提要
数学来源于生活，又应用于生活，当前的纳税，利息，分期付款，销售利润等问题都与一元二次方程有关，常见一元二次方程应用题类型有：①经营决策类；②平均增长率问题；③面积问题；④动态问题。解答这些问题时，不论背景如何复杂与变化，一定要抓住问题的关键，寻找等量关系，经过“问题情境-建立模型-求解-解释与应用”的过程，并注意根据实际意义对所列一元二次方程的解进行合理的取舍。
知识全解
一．列一元二次方程解实际问题的一般步骤
列一元二次方程解实际问题的一般步骤如下
（1）审题，找等量关系：通过审题，分清已知数和未知数，找出实际问题中的等量关系。
（2）设未知数
（3）列方程：根据等量关系列出所需的代数式，从而列出方程
（4）解方程：解这个方程，求出未知数的值
（5）验根：检验方程的解是否正确，是否符合题意
（6）答：写出答案
二．列一元二次方程解实际问题
（1）数字问题：①两位数可表示为十位数字×10+个位数字；②三位数可表示为百位数×100+十位数字×10+个位数字；③三个连续整数可表示为x-1，x，x+1；④三个连续奇数可表示为2x-1，2x+1，2x+3；⑤三个连续偶数可表示为2x-2，2x，2x+2。
（2）传播问题：第一轮1人影响n人，第二轮这（1+n）人再分别影响n人，经过两轮传播共有1+n+n(1+n)人受到影响。
方法点拨
类型1 数字问题
例1 有一个两位数，它的十位上的数字比个位上的数字小2，十位上的数字与个位上的数字的积的3倍刚好等于这个两位数，求这个两位数。
【分析】设个位数字为x，也可设十位数字为x，但为了表示十位数字顺利一些，设十位数字为x，再利用等量关系“十位上的数字与个位上的数字的积的3倍等于这个两位数”列出方程。
【解答】设十位上的数字为x，则个位上的数字为（x+2）。根据题意，得
3x(x+2)=10x+(x+2)
整理，得
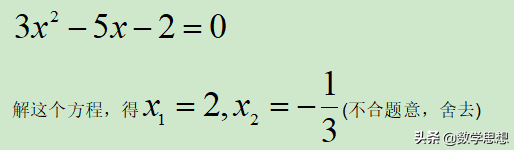
当x=2时， x+2=4
答：这个两位数是24。
【方法总结】数字问题一般涉及两个未知数，且相等关系中必有两数乘积运算。
类型2 传播问题
例2 有一人患了流感，经过两轮传染后共有64人患了流感
（1）求每轮传染中平均一个人传染了几个人
（2）如果不及时控制，第三轮将又有多少人被传染
【分析】设每轮传染中平均每人传染了x人，根据经过两轮传染后共有64人患了流感，可求出x，进而求出第三轮过后，又被感染的人数。
【解答】（1）设每轮传染中平均每人传染了x人
1+x+x(1+x)=64
整理，得x=7或x=-9(舍去)
答：每轮传染中平均一个人传染了7个人。
（2）64×7=448（人）
答：第三轮将又有448人被传染。
【方法总结】这类问题是近年中考的热点与亮点，尤其是病毒传播速度成几何级数增长，随着传播轮数的增加，数量是十分惊人的，一定要画好分析图，尤其是要弄清每轮传播的源头与传播后的总和。解这类问题的关键是理解题意，设出恰当的未知数列方程求解。
类型3 平均变化（增长）率问题
例3 某中心城市有一楼盘，开发商准备以每平方米7000元价格出售，由于国家出台了有关调控房地产的政策，开发商经过两次下调销售价格后，决定以每平方米5670元的价格销售
（1）求平均每次下调的百分率
（2）房产销售经理向开发商建议：先公布下调5%，再下调15%，这样更有吸引力，请问房产销售经理的方案对购房者是否更优惠？为什么？
【分析】（1）设平均每次下调的百分率为x，利用
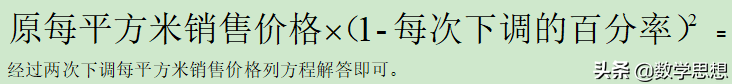
（2）求出先下调5%，再下调15%后的价格是原来价格的百分率，与开发商的方案比较，即可求解。
【解答】（1）设平均每次下调的百分率是x，根据题意列方程得，
类型4 几何图形方面的问题
例4 如下图，在一块长为22m，宽为17m的矩形地面上，要修建同样宽的两条互相垂直的道路（两条道路各与矩形的一条边平行），剩余部分种上草，使草坪面积为300平米。若设道路宽为xm，则根据题意可列出方程___
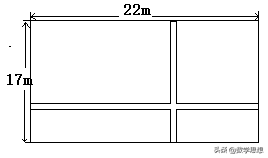
【分析】把所修的两条道路分别平移到矩形的最上边和最左边，则剩下的草坪是一个长方形，根据长方形的面积公式列方程即可。
【解答】设道路的宽应为xm，由题意有
(22-x)(17-x)=300
故答案为(22-x)(17-x)=300
【方法总结】解决面积问题的关键是将不规则图形分割或补全成规则图形，找出各部分面积之间的关系，运用面积公式列出方程。把中间修建的两条道路分别平移到矩形地面的最上边和最左边是解本题的关键。
类型5 销售利润问题
例5 百货大楼服装柜在销售中发现：某某牌童装平均每天可售出20件，每件盈利40元。为了迎接“十一”国庆节，商场决定采取适当的 降价措施，扩大销售量，增加盈利，尽快减少库存。经市场调查发现：如果每件童装降价4元，那么平均每天可多售出8件。要想平均每天在销售这种童装上盈利1200元，那么每件童装应降价多少？
【分析】每件的利润是（40-x）元，如果每件童装降价4元，那么平均每天可多售出8件，则件数为（20+8×(x/4)）件，抓住总利润列出方程进行求解。
【解答】设每件童装应降价x元，则（40-x）（20+8×(x/4)）=1200，解得x1=20，x2=10。
因为要尽快减少库存，所以x=20。
答：每件童装应降价20元。
【方法总结】本题主要的数量关系是销售利润=每件利润×件数，理解商品的销售的件数及商品价格的关系是解答本题的关键。数学来源于生活，又应用于生活，当前的纳税，利息，分期付款，销售利润等问题通常都与一元二次方程有关，解答这类问题时，不论背景如何复杂与变化，一定要抓住问题的关键，寻找等量关系，并注意根据实际意义对所列一元二次方程的解进行合理的取舍。
